2020年人教部编版初三下册数学期末模拟试题
名字：____________________班级：____________________[来源:学科网ZXXK]
1、选择题
1.3cosplay 30°的值是
A.6 B.6 C.6 D.3
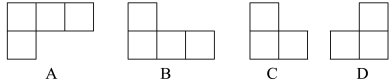
2．由五个相同的小立方块搭成的几何体如图所示，这个几何体的俯瞰图是
3．点A，B是反比率函数y＝x图象上的两点，则y1，y2的大小关系是
A．y1＞y2 B．y1＝y2
C．y1＜y2 D．不可以确定
4．有两个一样的三角形，已知其中一个三角形的最长边为12 cm，面积为18 cm2，而另一个三角形的最长边为16 cm，则另一个三角形的面积是
A．22 cm2 B．24 cm2
C．30 cm2 D．32 cm2
5．如图，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则∠BED的正切值等于
[来源:学科网ZXXK]
A.5 B.5 C．2 D.2
6．如图，点C在反比率函数y＝x的图象上，过点C的直线与x轴、y轴分别交于点A，B，且AB＝BC，△AOB的面积为1，则k的值为
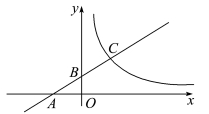
A．1 B．2 C．3 D．4
7．若函数y＝x与y＝ax2＋bx＋c的图象如图所示，则函数y＝kx＋b的大致图象为
8．如图所示，给出下列条件：①∠B＝∠ACD；②∠ADC＝∠ACB；③CD＝BC；④AC2＝AD·AB.其中可以单独断定△ABC∽△ACD的条件个数为
A．4 B．3 C．2 D．1
9．如图，菱形ABCD的边AD与x轴平行，A，B两点的横坐标分别为1和3，反比率函数y＝x的图象经过A，B两点，则菱形ABCD的面积是
A．4 B．4 C．2 D．2
10．如图，CB＝CA，∠ACB＝90°，点D在BC边上，四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q.给出以下结论：①AC＝FG；②S△FAB∶S四边形CBFG＝1∶2；③∠ABC＝∠ABF；④AD2＝FQ·AC.其中正确结论的个数是
A．1 B．2 C．3 D．4
2、填空题
11．在Rt△ABC中，∠C＝90°，AB＝20，sin A＝0.6，则BC＝______________.
12．如图，点A是函数y1＝－x图象上一点，连接AO交反比率函数y2＝x的图象于点B.若BO＝2AB，则k＝____________3__.
13．由一些一模一样的小正方体搭成的几何体的主视图和俯瞰图如图所示，则组成这个几何体的小正方体的个数可能是______________.
14．如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE∥AB交AC于点F，AB＝12，EF＝9，则DF的长是______________.
15．如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°.已知甲楼的高AB是120 m，则乙楼的高CD是______________m__________
16．如图，已知双曲线y＝x与直线y＝－x＋6相交于A，B两点，过点A作x轴的垂线与过点B作y轴的垂线相交于点C，若△ABC的面积为8，则k的值为______________.
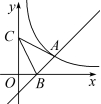
17．如图，一次函数y＝x－1的图象与反比率函数y＝x的图象在第一象限相交于点A，与x轴相交于点B，点C在y轴上，若AC＝BC，则点C的坐标为________________________
[来源:Zbase64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQH/2wBDAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQH/wAARCAADAAMDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBA人工智能RAxEAPwD+6n4NyPL8OtDkkbc7XXiLJwBnb4n1lRwAAMKAOB2ooor8/wDCdJeFvhukkkuA+EUkkkkv7Ay/RJWSXoexxFpn+eLtm+ZL/wAvKx//2Q==" />坐标为__，－4__.
3、解答卷
19．某工厂要加工一批茶叶罐，设计者给出了茶叶罐的三视图，如图所示，请你根据三视图确定制作每一个茶叶罐所需钢板的面积．
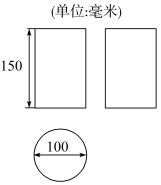
解：由三视图可知茶叶罐的形状为圆柱，并且茶叶罐的底面直径2r为100毫米，高h为150毫米．
∵每一个茶叶罐所需钢板的面积
即为该圆柱的表面积，
∴S表面＝2πr2＋2πrh＝2π×502＋2π×50×150＝20 000π．
答：制作每一个茶叶罐所需钢板的面积为20 000π平方毫米．
20．如图，在△ABC中，CD⊥AB于点D，tan A＝2cosplay∠BCD.
求证：BC＝2AD；
若cosplay B＝4，AB＝10，求CD的长．
解：证明：∵tan A＝AD，cosplay∠BCD＝BC，tan A＝2cosplay∠BCD，∴AD＝2·BC.∴BC＝2AD.
∵cosplay B＝BC＝4，BC＝2AD，∴AD＝2.
∵AB＝10，∴AD＝5×10＝4，BD＝5×10＝6，
∴BC＝8.∴CD＝＝2.
21．如图，已知平行四边形OABC中，点O为坐标顶点，点A，C，函数y＝x的图象经过点C.
求k的值及直线OB的函数分析式；
求四边形OABC的周长．
解：依题意，得点C在反比率函数y＝x的图象上，∴k＝xy＝2.
∵A，∴CB＝OA＝3.又CB∥x轴，∴B．
设直线OB的函数分析式为y＝ax，
∴2＝4a，∴a＝2，∴直线OB的函数分析式为y＝2x.
如图，过点C作CD⊥OA于点D.
∵C，∴OC＝＝.
在平行四边形OABC中，CB＝OA＝3，AB＝OC＝，
∴四边形OABC的周长为3＋3＋＋＝6＋2，
即四边形OABC的周长为6＋2.
22．小李要外出参加“建国70周年”庆祝活动，需网上购物一个拉杆箱，图1，2分别是她上网时看到的某种型号拉杆箱的实物图与示意图，并获得了如下信息：滑杆DE、箱长BC、拉杆AB的长度都相等，B，F在AC上，C在DE上，支杆DF＝30 cm，CE∶CD＝1∶3，∠DCF＝45°，∠CDF＝30°.请依据以上信息，解决下列问题．
求AC的长度；
求拉杆端点A到水平滑杆ED的距离．
解：如图，过点F作FH⊥DE于点H，
∴∠FHC＝∠FHD＝90°.∵∠FDC＝30°，DF＝30 cm，
∴FH＝2DF＝15 cm，DH＝2DF＝15 cm.
∵∠FCH＝45°，∴CH＝FH＝15 cm，
∴CD＝CH＋DH＝cm.
∵CE∶CD＝1∶3，∴DE＝3CD＝cm.
∵AB＝BC＝DE，∴AC＝cm.
[来源:学科网]
如图，过点A作AG⊥ED交ED的延长线于点G.
∵∠ACG＝45°，∴AG＝2AC＝cm.
答：拉杆端点A到水平滑杆ED的距离为cm.
23．如图，在正方形ABCD中，E是AB上一点，连接DE，过点A作AF⊥DE，垂足为F.⊙O经过点C，D，F，与AD相交于点G.
求证：△AFG∽△DFC；
若正方形ABCD的边长为4，AE＝1，求⊙O的半径．
解：证明：在正方形ABCD中，∠ADC＝90°，
∴∠CDF＋∠ADF＝90°.∵AF⊥DE，∴∠AFD＝90°，
∴∠DAF＋∠ADF＝90°.∴∠DAF＝∠CDF.
∵四边形GFCD是⊙O的内接四边形，
∴∠DCF＋∠DGF＝180°.又∠AGF＋∠DGF＝180°，
∴∠AGF＝∠DCF.∴△AFG∽△DFC.
如图，连接CG，∵∠CDG＝90°，
∴CG为⊙O的直径．
∵∠AFE＝∠DAE＝90°，∠EAF＋∠AEF＝90°，
∠DAF＋∠EAF＝90°，∴∠AEF＝∠DAF，
∴△AFD∽△EAD，∴DF＝AD.
∵△AFG∽△DFC，∴DC＝DF，∴DC＝AD.
在正方形ABCD中，AD＝CD，
∴AG＝AE＝1，DG＝AD－AG＝4－1＝3.
∴CG＝＝＝5.
∴⊙O的半径为2.
24．如图，已知反比率函数y＝x的图象与反比率函数y＝x的图象关于y轴对称，A，B是函数y＝x图象上的两点，连接AB，点C是函数y＝x图象上的一点，连接AC，BC.
求m，n的值；
求AB所在直线的分析式；
求△ABC的面积．
解：∵A，B是函数y＝x图象上的两点，∴，解得m＝1，
∴反比率函数y＝x的分析式为y＝x.
∵反比率函数y＝x的图象与反比率函数y＝x的图象关于y轴对称，点C是函数y＝x图象上的一点，∴点C关于y轴的对称点肯定在反比率函数y＝x的图象上，
∴n＝2＝2.
∵m＝1，∴点B的坐标为．
设AB所在直线的分析式为y＝kx＋b，由题意得
k＋b＝4，解得b＝5，
∴AB所在直线的分析式为y＝－x＋5.
如图所示，过点A，B，C作AD⊥x轴于点D，BE⊥x轴于点E，CF⊥x轴于点F.[来源:Zxxk.Com]
∵A，B，C，
∴AD＝4，BE＝1，CF＝2，DE＝3，DF＝3，EF＝6，
∴S△ABC＝S梯形ADFC＋S梯形ADEB－S梯形BCFE
＝2××3＋2××3－2××6
＝9＋7.5－9＝7.5.
25．如图，Rt△ABC中，∠ACB＝90°，AC＝BC，P为△ABC内部一点，且∠APB＝∠BPC＝135°.
求证：△PAB∽△PBC；
求证：PA＝2PC；
若点P到三角形的边AB，BC，CA的距离分别为h1，h2，h3，求证h1＝h2·h3.
证明：∵∠ACB＝90°，AC＝BC，
∴∠ABC＝45°＝∠PBA＋∠PBC.
又∠APB＝135°，∴∠PAB＋∠PBA＝45°，
∴∠PBC＝∠PAB.
又∵∠APB＝∠BPC＝135°，∴△PAB∽△PBC.
∵△PAB∽△PBC，∴PB＝PC＝BC.
在Rt△ABC中，∵AC＝BC，∴BC＝，
∴PA＝PB，PB＝PC，∴PA＝2PC.
如图，过点P作PD⊥BC，PE⊥AC，PF⊥AB，分别交BC，AC，AB于点D，E，F，
∴PF＝h1，PD＝h2，PE＝h3.
∵∠CPB＋∠APB＝135°＋135°＝270
°，
∴∠APC＝90°，∴∠EAP＋∠ACP＝90°.
又∵∠ACB＝∠ACP＋∠PCD＝90°，
∴∠EAP＝∠PCD，
∴Rt△AEP∽Rt△CDP，
∴DP＝PC＝2，即h2＝2，∴h3＝2h2.
∵△PAB∽△PBC，
∴h2＝BC＝，∴h1＝h2，
∴h1＝2h2＝2h2·h2＝h2·h3，即h1＝h2·h3.
